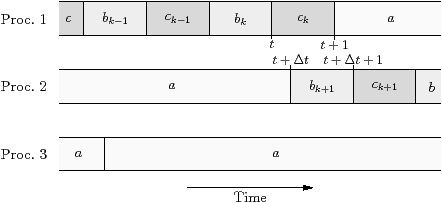
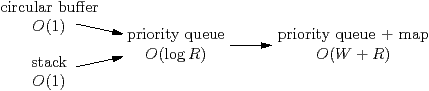Chapter 4 Run-time Decisions
The previous chapter introduced two new algorithms for the stream compiler.
The stream compiler transforms the source code into an executable, performing
optimisations using the information known before the program starts running.
This chapter focuses instead on the decisions taken at run time. In
particular, this chapter is concerned with dynamic scheduling of stream
programs.
A program can be scheduled either statically, by the compiler, or dynamically,
by the run-time system. Chapter 3 was concerned with static
scheduling. If the program is scheduled statically, each task becomes a thread
containing a loop, each iteration of which executes its kernels’ work functions
in sequence. Tasks communicate using communications primitives, which they
call as and when they need them. This implies a relatively simple run-time
system, similar to acolib. The main advantages of static scheduling are
low overhead and low memory use.
If the program is scheduled dynamically, each task is broken up into
self-contained, non-blocking tasks. The dynamic scheduler decides in which
order to run these tasks, constrained by dependencies between them: a task
cannot start if it needs an output from a task that hasn’t yet finished. Tasks
consume input when they start and produce output when they complete, rather
than communicating as required using communications primitives.
Dynamic scheduling is the only choice when the program’s behaviour is
unpredictable. It also supports stream graphs that are not known at compile
time, because kernels and streams are introduced dynamically. As illustrated
in Figure 4.1, a dynamic scheduler adds overhead, but it
can be better overall when the partitioned stream program is unbalanced. The
discussion in Section 4.2.2 gives an example.
A dynamically scheduled program still benefits from unrolling and partitioning
transformations, since they coarsen the granularity, and bigger tasks have
smaller total overhead. In addition, unrolling enables vectorisation, and task
fusion enables data reuse and polyhedral transformations. A partitioning
transformation for a dynamic scheduler, unlike the algorithm in
Chapter 3, does not need to map tasks to processors.
Section 4.1 defines the dynamic scheduling problem.
Section 4.2 describes the previously known scheduling
algorithms, and gives a worst case example for each.
Section 4.3 develops an adaptive scheduler for
stream-like applications. There are two variants of this scheduler, the
apriority stream scheduler requires a one-dimensional stream program,
and it needs annotations from the compiler. The gpriority
general-purpose scheduler is more general, and it does not need any additional
information. Section 4.4 is the experimental evaluation.
| | Balanced program | Unbalanced program |
| |
Static schedule | | |
| |
Dynamic schedule | | |
| | ⇒ static schedule is shorter | ⇒ dynamic schedule is shorter |
| Figure 4.1: Example traces with static and dynamic scheduling (black is scheduling overhead and
shades distinguish kernels) |
4.1 The dynamic scheduling problem
4.1.1 Interface to the dynamic scheduler
The stream program starts executing on one processor, in a sequential master
thread. Whenever the master thread reaches a function marked as a task, the
function does not execute right away. Instead, an instance of that task is
created, and added to the partially-generated dependency graph (PDG).
The PDG holds tasks until they have finished executing. Each vertex is a task,
and each directed edge represents a dependency between tasks. When the
predecessors of a task, if any, have all finished, the task becomes
ready. Ready tasks are held in a data structure known as the
ready queue, until they are issued, in an order determined by the
dynamic scheduler. Figure 4.2 illustrates this process,
showing the dynamic scheduler in context.
The dynamic scheduler supports the three operations labelled in
Figure 4.2:
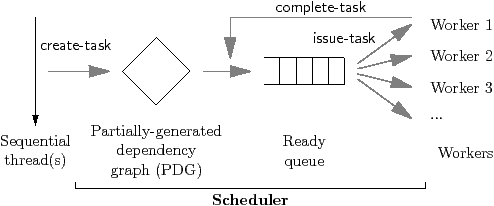
| Figure 4.2: Dynamic scheduler in context |
| void create-task(Task task-id, Task-set preds) |
| Task issue-task(Worker worker) |
| void complete-task(Task task-id) |
-1 The create-task operation adds a task to the partial
dependency graph (PDG). Its arguments identify the task, and the
set of tasks whose outputs it consumes. The issue-task operation is
called by a worker when it is idle; it waits for and returns the next ready
task to issue. The complete-task operation is called by a worker when
it finishes executing its task; it notifies the scheduler that the outputs from
that task are now ready. A complete scheduler would provide some additional
operations, to support initialisation, barriers, and so on, but they are not
relevant here. This interface is similar to the interface between
Nanos++ [Nana] and its scheduler plugin.
-1 This construction has some direct implications. First, tasks are
non-preemptive, so once issued, they run to completion. Second, the
scheduler is non-clairvoyant, meaning that task execution times are
not known until they complete. Third, the dependency graph is built by a
sequential thread, and is not known all at once.
4.1.2 Throttle policy
Another aspect of scheduling is the throttle policy. The program may
create a large number of tasks in the course of its execution, so the main
thread should be stalled if the PDG contains too many tasks. On Nanos++, this
is done by inlining the next task, effectively making the rest of the master
thread a new task dependent on the newly created one. This is a reasonable
way to prune a recursive computation such as quicksort, which would otherwise
create a large number of very small tasks. On CellSs, the main program on the
PPE simply stalls, and the processor does not become an extra worker, since all
the workers are SPEs.
The decision to stall task creation is taken by the throttle policy. In
Nanos++, the default throttle policy is based on the number of ready tasks per
processor, inlining tasks if the number of ready tasks is greater than some
threshold.
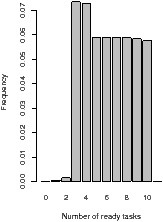
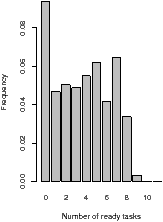
For one-dimensional stream programs, the number of ready tasks is usually
confined to a relatively narrow region, as shown in the histograms in
Figure 4.3. These histograms show the distribution of the
number of ready tasks, sampled at a constant rate. If the threshold is greater
than ten, it is never exceeded, and the size of the PDG will grow without
limit. If it is less than ten, the main thread will stall too frequently. A
better throttle policy is one based on the number of tasks in the PDG. The
main thread should be stalled when the PDG contains a certain number of
iterations’ worth of tasks.
 |  | 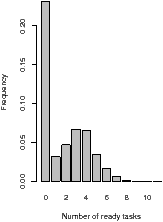 |
| (a) 1 processor | (b) 6 processors | (c) 16 processors |
| Figure 4.3: Number of ready tasks, excluding those running: channelvocoder, using oldest-first |
4.1.3 Objective function: comparing schedulers
The precise goal of the scheduler depends on the context. An offline
stream program, such as video transcoding or a database query, should be
finished as soon as possible. In standard terminology, the scheduler’s
objective would be to minimise the makespan, written Cmax, the time that
the last task finishes.
Other stream programs, such as video playback, operate in real time. This
suggests that an additional goal should be to minimise latency, so that an
output frame isn’t delayed by the processing of too many tasks from future
frames.
An additional constraint on the scheduler is memory footprint. If the memory
footprint is too large, either performance will suffer through paging to disk,
or the program will fail due to insufficient memory.
4.2 Survey of DAG scheduling techniques
The scheduling problem is NP-hard, because it includes a well-known
NP-hard problem as a special case. This corresponds to the case
where the dependency graph is known up-front, a problem known as
p | prec | Cmax [LK78, Ull75].1 The scheduler therefore
has to use a heuristic, which tries to find a good solution that might
not be optimal. Many heuristics have been proposed, for various related
scheduling problems, and a selection is given in Table 4.1.
Many of these heuristics are unsuitable because they require the task execution
times, they need to schedule the whole program in advance, or they are too slow.
| Abbrev. | Full name | Year | Online? | | Heterogeneous? | Clairvoyant | Note |
| HLFNET [ACD74] | Highest Levels First with No Estimated Finish Times | 1974 | Offline | | Homo | No | Same as botlev |
| SCFNET [ACD74] | Smallest Co-levels First with No Estimated Finish Times | 1974 | Online | | Homo | No | Same as toplev |
| DSH [KL88] | Duplication Scheduling Heuristic | 1988 | Offline | | Homo | Yes | O(n4) is too slow |
| ETF [HCAL89] | Earliest Task First | 1989 | Online | | Homo | No | Schedules task that would start first |
| MCP [WG90] | Modified Critical Path | 1990 | Offline | | Homo | Yes | Like botlev, but takes account of descendants’ bottom levels |
| MH [ERL90] | Mapping Heuristic | 1990 | Offline | | Hetero | Yes | O(n2p3) is too slow |
| GDL [SL93] | Generalised Dynamic Level | 1993 | Offline | | Hetero | Yes |
| DSC [YG94] | Dominant Sequence Clustering | 1994 | Offline | | Homo | Yes |
| BIL [OH96] | Best Imaginary Level | 1996 | Offline | | Hetero | Yes |
| HEFT [THW99] | Heterogeneous Earliest Finish Time | 1999 | Offline | | Hetero | Yes |
| MCT [MAS+02] | Minimum Completion Time | 1999 | Online | | Hetero | Yes |
| MET [MAS+02] | Minimum Execution Time | 1999 | Online | | Hetero | Yes |
| PCT [MAS+02] | Partial Completion Time | 1999 | Online | | Hetero | Yes |
| OLB [MAS+02] | Opportunistic Load Balancing | 1999 | Online | | Hetero | Yes |
| CPOP [THW99] | Critical Path on a Processor | 1999 | Offline | | Hetero | Yes |
| k-DLA [WY02] | k-Depth Lookahead | 2002 | Offline | | Hetero | Yes |
| HCPT [HJ03] | Heterogeneous Critical Parent Trees | 2003 | Offline | | Hetero | Yes |
| Table 4.1: Known DAG scheduling heuristics, related to the problem in this chapter |
This section investigates the performance of the scheduling algorithms listed
in Table 4.2. These policies are non-preemptive, non-clairvoyant,
online, and fast. The next subsection describes the policies in detail.
Subsection 4.2.2 gives a simple realistic worst-case example for
each policy. Subsection 4.4 is an empirical analysis on a
16-core machine.
Policy | Description | Priority known when | Priority at ready time | Ready queue | Ties possible | Per-task complexity |
fifo | FIFO (ready-first) | ready | known | circular buffer | yes | O(1) |
lifo | LIFO (ready-last) | ready | known | stack | yes | O(1) |
oldest | Earliest created task first | created | known | priority queue | no | O(logR) |
toplev | Minimum top level (depth) | created | known | priority queue | yes | O(logR) |
botlev | Maximum bottom level | issued | lower bound | priority queue + map | yes | O(W) |
crit | Maximum top+bottom level | issued | lower bound | priority queue + map | yes | O(W) |
mchild | Maximum number of children | issued | lower bound | priority queue + map | yes | O(logR) |
mdesc | Maximum num. descendants | issued | lower bound | priority queue + map | yes | O(W) |
wave | Stream program wavefront | created | known | priority queue | yes | O(logR) |
apriority | | ready | known | priority queue | yes | O(logR) |
gpriority | | ready | known | priority queue | yes | O(logR) |
| Table 4.2: The scheduling policies and cost, where W is the number of tasks in the PDG, and R is the number of ready tasks |
4.2.1 The online scheduling policies
Table 4.2 lists the scheduling policies investigated in this
section. All policies work by issuing a ready task with the highest
priority, where the priorities may be adjusted dynamically, and they
differ, of course, between the policies. It is possible to construct examples
that cannot be scheduled optimally by any priority-based
scheduler [Koh75], since the optimal schedule may require
unforced idle time: a processor waiting idle for some time, even though
there are some ready tasks. Section 4.2.2 gives an example stream
program, observed in practice, which has poor performance for this reason, when
using the oldest-first scheduler.
| | | Top level | Bottom level | Criticality | #Children | #Descendants |
| A | 5*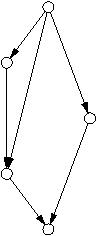 | 0 | 3 | 3 | 3 | 4 |
| B | | 1 | 2 | 3 | 1 | 2 |
| C | | 1 | 1 | 2 | 1 | 1 |
| D | | 2 | 1 | 3 | 1 | 1 |
| E | | 3 | 0 | 3 | 0 | 0 |
| Figure 4.4: Metrics used by the scheduling policies |
The fifo (first in–first out) policy schedules the task that
became ready first. Conversely, the lifo (last
in–last out) policy schedules the one that became ready last. For
recursively generated computations, such as quicksort, fifo tends to
open up parallelism, because it schedules larger tasks near the top of the call
tree first, doing the computation in breadth-first order. In contrast,
lifo has lower memory use and better data locality, and would often be
the best schedule for a single processor. The Cilk
scheduler [BJK+95] uses LIFO for local queues and FIFO for work
stealing.
The oldest policy schedules the task that was created
first. This policy is similar to FIFO when all tasks are independent.
The remaining policies use the metrics illustrated in Figure 4.4.
The toplev policy schedules a task with the minimum top
level; the top level is the number of edges in a longest path from a source
vertex to the task. Similarly, the botlev policy schedules a
task with the maximum bottom level, which is the number of edges in a
longest path from the task to a sink vertex. The toplev and
botlev policies are also called SCFNET and HLFNET,
respectively [ACD74]. The botlev policy was used for
task scheduling in 1969 [Bow69], and later, when taking account of
known computation times, it was known as HLFET and the Critical Path Method.
There is an important difference between the top and bottom levels. The top
level is easily calculated in task creation, and is then known for certain, but
the bottom level must be calculated bottom up. Adding a task to the PDG may
change the bottom level of every other task. The average case will normally be
less expensive, since the traversal can terminate whenever it reaches a task
whose bottom level is not changed. The bottom levels may be updated in this
way, either every time a task is created, or periodically.
The crit policy schedules a task with the maximum
criticality, which is the sum of the top and bottom levels. The
crit policy is equivalent to choosing a task with the least
slack (sometimes called the mobility). The mchild
policy schedules a task with the greatest number of successors. The aim is to
try to open up parallelism, but the policy is short-sighted because it is
local, and it is not adaptive, because it keeps opening up parallelism even if
there is plenty enough already. The mdesc policy schedules a
task with the greatest number of descendants. It is expensive and has poor
performance.
The wave scheduler is specific to one dimensional stream
programs. It schedules a kernel with lowest wave number, where the wave number
of a kernel is equal to the iteration number plus the kernel’s top level within
the iteration. It is equal to the top level when all kernels have multiplicity
one.
The apriority and gpriority policies are
the adaptive schedulers that will be introduced in
Section 4.3. The results are presented in this section
so they can be more easily compared with the existing schedulers.
All policies except oldest-first may give several tasks the same priority.
Often the tie will be broken in some arbitrary way, but this could be done
using a second scheduling policy. Continuing like this, a heuristic is
a list of policies; e.g. (fifo, oldest) is a FIFO scheduler,
but if several tasks became ready at the same time, they are scheduled in
increasing order of their creation time.
Scheduler complexity
Table 4.2 summarises the overall amortised per task time complexity
of the policies. The complexity takes account of the cost of assigning
priorities, updating priorities when other tasks are created, and pushing and
popping tasks to the ready “queue”.
The table shows the ready “queue” data structure required by each
policy. The fifo policy, on its own, simply uses a circular buffer
for the ready queue. There is no need to explicitly track priorities, because
the priority of a task is known when it becomes ready, and is implied by its
position in the circular buffer. Similarly, lifo uses a stack. For
fifo and lifo, insertion and removal are both constant time:
O(1).
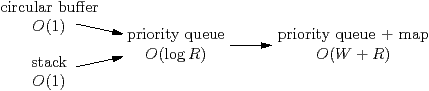
| Figure 4.5: Lattice of ready queues for a heuristic |
The oldest, toplev and wave policies use a priority
queue, because the task’s priority is known at creation time, and therefore
known at ready time, when the task is inserted into the queue. Similarly for
apriority and gpriority. Both insertion and removal have
cost O(logr), using a heap or self-balancing binary tree, where r is the
current size of the ready queue. The average value of logr is written
logR. In both cases, calculating the priority itself is
constant time: O(1), so overall the cost per task is logR.
For the remaining policies, task priorities are not known until issue time, but
a lower bound is known at ready time. For example, the mchild policy
schedules the task with the greatest number of children. When a task becomes
ready, some of its children may already have been created, but not always all
of them. Each time another task is created, all of its parents require their
priority to be increased by one. The number of ready parents is at most the
number of function arguments, so the extra number of updates per task is
O(1).
These policies can be implemented using a priority queue, since priority queues
typically provide an operation that increases an element’s priority. It also
requires a map from the task ID to its position in the priority queue; e.g. the
node in a tree, and this map must be updated as the priority queue is
manipulated. Task removal has cost O(logr), as before, but task creation
requires some of the priorities of the tasks in the ready queue to be updated.
Using a balanced tree or heap, updating the priority of a single task in the
ready queue is O(logr); using a Fibonacci heap, it is O(1) amortised
time [FT87a].
For botlev, crit, and mdesc, adding a single task
may change the priority of every other task in the PDG. There are simple,
common, examples, for each of the three policies, that exhibit this worse case.
A heuristic is a list of policies, and the ready queue for a heuristic is the
most general of the ready queues of its policies; i.e. the one that is
furthest to the right of Figure 4.5.
2*Heuristic | Throughput (compared with optimal) |
| | Exhaustion | Back pressure |
Optimal static, without fission | 1/p | n/a |
Optimal static, with fission | p+1/2p | n/a |
(oldest) | p/2p−1 | 3p−4/2p−2 |
(fifo, *) | p/2p−1 | 2p/3p−1 |
(lifo, *) | n/a | p/2p−1 |
(toplev, *) | p/2p−1 | p/2p − 1 − f* |
(botlev, *) | p/2p−1 | p/2p − 1 − f* |
(crit, *) | p/2p−1 | p/2p−1 |
(mchild, *) | p/2p−1 | p/2p−1 |
(mdesc, *) | p/2p−1 | p/2p − 1 − f† |
(wave, *) | n/a | n/a |
| Table 4.3: Throughput for one dimensional stream programs, compared with optimal, where
p is the number of processors,
f is the unroll factor,
f* = p−1/f, f†= p−1/f+1 |
4.2.2 Theoretical evaluation
This section exhibits simple, realistic worst case examples for the scheduling
heuristics. Many of these examples occur in the results in
Section 4.4. All the examples are one-dimensional
“streaming” programs, constructed by a single for loop containing
calls to several kernels. Each such call generates a task. The
multiplicity, or number of tasks per kernel per iteration,
varies between kernels.
These streaming examples divide into two groups, which correspond to the two
main ways that the schedule can be bad. The first group suffers from
exhaustion, meaning that the scheduler frequently runs out of
parallelism throughout the execution. This happens when the scheduler tends to
complete all the kernels from one loop iteration before starting the next
iteration. This is typical of oldest, and it is inappropriate when
the next iteration begins with a long kernel, on which all other kernels
depend.
-1 The second group suffers from poor back pressure, meaning
that some kernels execute the loop iterations at a faster rate than others.
Poor back pressure implies poor temporal data locality, which, if the amount of
data transferred between kernels is large, will reduce performance
significantly. If the amount of data transferred is small, when all iterations
of the faster kernels have been done, there may not be enough parallelism left
to keep all of the processors busy. Back pressure can be helped by reducing
the window size, but it still uses more memory than it should; exhaustion
cannot.
Table 4.3 shows the worst case throughput, as a
multiple of the optimal throughput. These figures assume that the number of
iterations are large, so they exclude the overhead at the start and end of the
program. All examples have an optimal schedule with all processors 100% busy
during the steady state.
Many examples have worst case ratio close to p/2p−1, so for large
numbers of processors, on average they use only half of the number of
processors as the optimal schedule. Graham’s bound [Gra71]
shows that any demand scheduler; i.e. one using priorities or a list schedule,
has execution time at most 2p−1/p times optimal; so this bound is
indeed the worst case.
These examples are synchronous dataflow (SDF) [LM87] streaming
programs, so they could also be scheduled statically, at compile time.
Table 4.3 shows the worst case for optimal
static schedulers with and without support for kernel fission, which
splits stateless kernels (a kernel is stateless if there is no dependency path
from one iteration of the kernel to another).
If the static scheduler does not support fission, the worst case is when
most of the work is in a single stateless kernel, since the static scheduler
allocates that kernel to one of the processors, while any dynamic scheduler
would run it on them all. With kernel fission, the worst case is a
pipeline of p+1 stateful kernels. One processor must be assigned two of
them, giving utilisation p+1/2p, which approaches one half for large
p.
| |
| |
(a) oldest | (b) botlev (inside nodes) and crit (outside) |
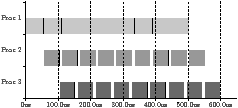
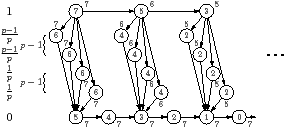
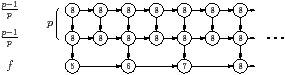
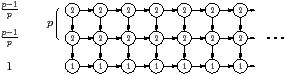
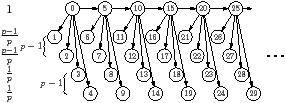
| Figure 4.6: Worst case examples for exhaustion, illustrated for p=3 processors |
Exhaustion
Figure 4.6(a) is an example where the
oldest policy suffers from exhaustion. The iterations of the
loop run from left to the right. Each row is a kernel, all of whose tasks have
the same execution time, shown to the left of the diagram. The vertex labels,
for this one diagram, number the tasks in the order they were created.
The other diagrams will highlight whichever metric is used by the scheduler.
The diagram is illustrated for p=3 processors.
An optimal schedule allocates one processor to the top row, at cost 1 per
iteration. The remaining p−1 processors are each allocated to one row of
cost p−1/p and one row of cost 1/p, for a total cost per
processor also equal to 1 per iteration. The schedule is a pipeline of
length two, and the loads are balanced, so steady state utilisation is 100%.
-1 The oldest scheduler will first issue task 0 from the
top row. Once that has completed, all other tasks in the same iteration (1,
2, 3, and 4 in the picture) become ready. The next task from the top row,
5, also becomes ready, but it will not be issued until the tasks from the
same iteration have been done. The kernel execution times have been chosen so
that all processors finish the first iteration at the same time. At this
point, the first task, 5, in the next iteration can start on one processor,
but the remaining processors will be idle.2 Each
iteration requires time 1 for the task from the top row, plus time
p−1/p for the remaining tasks; hence the result in
Table 4.3.
This example is a perfectly ordinary stream program, and several StreamIt
benchmarks suffer a similar fate. The fm benchmark illustrated in is
a good example.
This example can be adapted for some of the other heuristics. It works as it
stands for (fifo, oldest) and (lifo,
oldest), because in the above description, all tasks in the ready queue
became ready at the same time. To produce a general example for
fifo and toplev, add a zero-cost task
between each consecutive pair of tasks in the top row; i.e. between tasks 0
and 5, and 5 and 10; and so on.
-1 Figure 4.6(b) shows a similar example
for botlev and crit. The labels inside the
tasks are the bottom level, and the labels outside are the criticality. The
analysis is the same as before, and this example also turns up in the empirical
analysis. Similar examples exist for mchild and
mdesc. A possibility for the latter is to unroll all but the
first kernel and make the branches of the split stateful; this is one of many
ways to ensure that the branches of the split have more descendants than the
next task in the top row.
| |
| |
(a) toplev | (b) botlev (inside nodes) and mdesc (outside) |
| |
| |
(c) crit | (d) mchild and lifo |
| |
| |
(e) oldest | |
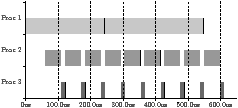
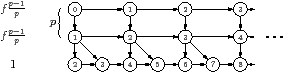
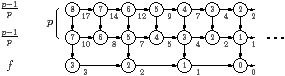
| Figure 4.7: Worst case examples for back pressure, illustrated for p=2 processors (p=3 for subfigure (e)) and unroll factor f=2 |
Back pressure
Figure 4.7(a) is an example where
toplev suffers from poor back pressure. Each task is
labelled with the top level. There are p+1 kernels, the first p of them
with multiplicity one, and the last with multiplicity f. The diagram is
illustrated for p=2 processors, and f=2. The first p rows have tasks of
cost f(p−1)/p, after unrolling, and the final row has tasks of cost 1.
An optimal dynamic schedule uses p−1 processors for the top p rows, and the
remaining processor for the bottom row. The bottom row has cost 1 per
iteration of the original loop. The tasks in the top p rows each have cost
f(p−1)/p, but they each cover f iterations of the original loop. Hence the
total cost for f iterations of the top p rows is f(p−1), which is also
1 per processor per original iteration. Ignoring the first few and last few
iterations, the load is balanced perfectly, and can be scheduled as a pipeline,
so utilisation is 100%.
The toplev scheduler proceeds by top level, with 100% utilisation
until the last task in the top row has been completed. At that point, the top
p rows are all close to complete, but the bottom row is about 1/f complete.
The rest of the bottom row will be serialised.
For n complete iterations of the original loop, the total busy CPU time, for
either scheduler, is np. The toplev scheduler has idle time equal to
|
t = (p−1)n | ⎛
⎜
⎜
⎝ | 1− | | ⎞
⎟
⎟
⎠ | ,
|
since p−1 processors wait for the completion of the bottom row.
The ratio of total time is therefore
For large unroll factors, the relative utilisation
is close to p/2p−1, itself close to one half for large numbers of
processors.
-1 Figure 4.7(b) is a similar example for
botlev and mdesc. The labels inside the
tasks are the bottom level, and the labels outside are the number of
descendants. The analysis is similar to the previous case, leaving much of the
bottom row to be processed sequentially on one processor. For
botlev, the bottom row will not be started until only 1/f of
the top row is left. At this point, the p+1 rows will be processed together,
until just the bottom row is left. For mdesc, the bottom row will
begin execution a little later, but the analysis is similar.
-1 Figures 4.7(c) and (d) show worst-case
examples for crit, and mchild and
lifo. The labels inside the tasks are the priorities, given
by the criticality and number of children, respectively. In both cases, none of
the tasks from the bottom row will be issued until the top row is finished.
For crit, this is true whatever the unroll factor, because
removing just one task from the bottom row moves the bottom row off the
critical path. For mchild, this is true because the tasks in the
bottom row have one child, whereas all the other tasks have two.
For lifo, the first or second task in the bottom row will be delayed
until the end of the execution, because it will always have been the first task
put in the ready queue that has still to be done.
For fifo, the utilisation under exhaustion is slightly higher, at
2p/3p−1. An example is a stateful pipeline, similar to
Figure 4.7(d), but with p(p−1) kernels of cost 1,
followed by a single high-cost kernel of cost p+є, for small
є. An optimal schedule has a perfectly balanced pipeline, processing
one iteration every p time units.
The fifo schedule, however, runs the high cost kernel at one half the
rate of the other kernels. The remaining iterations of this kernel will have
to be processed on one processor. This is because while a high-cost task is
executing, a complete wave of other tasks can complete: in time p on p−1
remaining processors, p(p−1) tasks are completed. When the high-cost task
has completed, there is a whole new wave of other tasks in the FIFO queue ahead
of it, so a second wave completes before the next high-cost task starts. The
utilisation, in Table 4.3, is like toplev with
f=2.
| |
(a) Stream graph | (b) Stealing the next kernel b |
| Figure 4.8: Illustration for oldest back pressure |
Surprisingly perhaps, the oldest scheduler can also suffer
from poor back pressure. This is possible, even though it always assigns
highest priority to the oldest task. An example is shown in
Figure 4.7(e). This example is redrawn in
Figure 4.8(a) as a stream graph, with the kernels labeled
a, b, and c.
The costs are chosen so that the optimal schedule should use, on average, one
processor for kernel b, one processor for c, and the rest of
the processors for kernel a.
In fact, the oldest scheduler often uses one processor for both
b and c, and p−1 instead of p−2 processors for the rest,
causing the back pressure problem. Figure 4.8(b) shows why.
When processor 3 finishes a task, processor 1 is currently executing an
iteration of kernel b, and no iterations of either kernel b or c are
ready. It therefore has to execute another iteration of kernel a. When
processor 2 finishes its task, processor 1 is currently executing kernel c,
and the next iteration of kernel b is ready. This allows processor 2 to
begin executing this kernel, opening up parallelism. However, when processor 1
finishes, the only ready tasks are again those from kernel a. The overlap is
therefore short-lived, and only in exceptional runs are there are a significant
amount of concurrency between kernels b and c.
4.3 Adaptive schedulers
This section describes two adaptive schedulers for stream-like programs. The
first, adaptive priority (apriority), is specific to
one-dimensional stream programs. The second, general adaptive priority
(gpriority), has slightly more overhead but it is more general.
Both policies are low overhead, and are based on the oldest-first scheduler.
As will be seen in Section 4.4, oldest-first has the
lowest memory use, and it usually has the best performance, but it sometimes
suffers from exhaustion. The adaptive schedulers modify the oldest first
scheduler so that if exhaustion occurs, the priorities are adjusted to try to
stop it happening again. If exhaustion never happens, both policies remain the
same as oldest throughout execution, retaining its low memory use.
The oldest scheduler issues the task with the smallest task number;
that is, the priority is zero minus the task number. Both the adaptive
schedulers modify this priority by adding an adjustment, which depends
only on the kernel ID. The adjustments start at zero. Whenever a kernel is
seen to be a bottleneck, the adjustments of that kernel and its ancestors are
increased.
Both adaptive schedulers have complexity similar to that of oldest-first. They
hold the ready tasks in a priority queue, which has complexity per task equal
to the average value of the logarithm of the number of ready tasks. Ready
tasks are inserted with known priority. The schedulers maintain a small table
of metrics, described later, which is updated in constant time per task. The
priority adjustments are updated infrequently, and the cost is linear in the
number of kernels. In addition, the gpriority scheduler has some
overhead at task creation time, which has a constant cost per dependency edge.
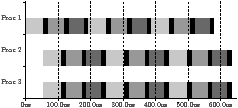
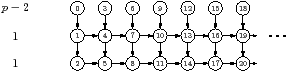
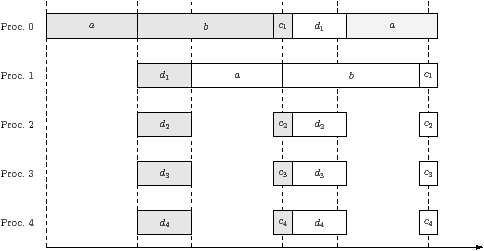
Figure 4.9 shows the worst-case example for oldest-first,
from Figure 4.6(a), redrawn as a stream graph, with
the kernels given labels a, b1, and so on. An execution trace is shown in
Figure 4.9(b). For comparison, an optimal execution
trace is shown in Figure 4.9(c). As described in
Section 4.2.2, this example suffers from exhaustion: processor
utilisation is poor because the oldest-first scheduler finishes the tasks from
one iteration before starting the next. The next iteration starts with a
single expensive kernel a, and all other processors have to wait for it to
finish.
The problem is apparent in the trace—only one processor is busy just before
kernel a finishes. To avoid this problem, each firing of kernel a should
have started executing earlier. In contrast, every time kernel b1 finishes
executing, roughly half of the processors are busy. The precise number depends
on the order in which b1 through b4 and c4 finish, and on the latency
in the run-time system between the time a task finishes and the thread is
marked idle. Figure 4.10 is an example set of statistics
after three iterations. It gives, for each kernel, the number of times that
kernel has been done and the average number of threads that were busy just
before it finished.
The average number of busy threads for kernel a is low, so a is probably
the bottleneck. The problem can be alleviated or fixed by increasing kernel
a’s priority. The following sections extend this idea into a working
scheduler.
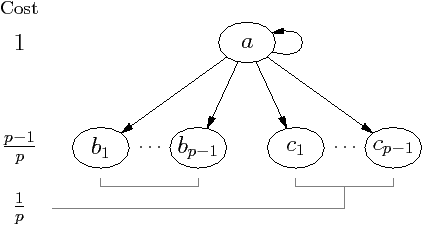
(b) Stream graph for example in Figure 4.6(a) for five processors
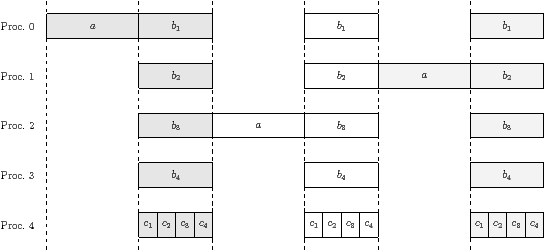
(b) Example execution trace for five processors (shading distinguishes iterations)
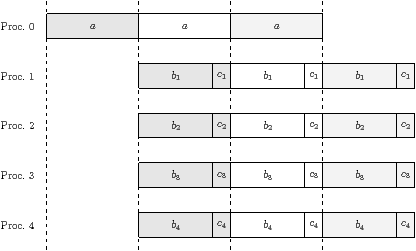
(c) Optimal execution trace for five processors (shading distinguishes iterations)
| Figure 4.9: Motivation for busyness statistic |
| Kernel | Times completed | Average busy threads |
| a | 3 | 1.0 | ← |
| b1 | 3 | 2.3 |
| b2 | 3 | 4.3 |
| b3 | 3 | 4.3 |
| b4 | 3 | 3.7 |
| c1 | 3 | 5.0 |
| c2 | 3 | 5.0 |
| c3 | 3 | 5.0 |
| c4 | 3 | 3.0 |
| Figure 4.10: Example statistics after three iterations of
the program in Figure 4.9 |
4.3.2 Monitoring
| Name | Notation | Initial value | Description |
| For every thread |
| State | Sj | not started | State: not started, busy, or idle |
| For every kernel |
| Adjustment | ak | 0 | Priority adjustment for this kernel |
| Sum busy threads | tk | 0 | Used to calculate average busy threads |
| Starved count | sk | 0 | Number of times kernel was starved |
| Non-starved count | ck | 0 | Number of times kernel has completed without being starved |
| Table 4.4: Statistics for adaptive schedulers |
Updating statistics
Table 4.4 lists the small set of statistics that are
maintained by the apriority and gpriority schedulers. Each
worker thread starts in state not started, in which it remains, until
the scheduler issues the first task to run on it. In order to avoid
discriminating against kernels near the top of the stream graph during the
first few iterations, processors are also considered busy if they have not
executed any tasks yet. The scheduler keeps track of the number of busy
threads, which is the number of threads in the not started or
busy state.
Every time a task completes, the adaptive scheduler needs to update the
corresponding kernel’s statistics. This must be done before any successors of
the task can become ready. If the next task for the same kernel has not yet
been created, the kernel is said to be starved, and the master thread
could be the bottleneck. If this happens too often, there would probably be
little point in increasing that kernel’s priority anyway. If the kernel is
starved and there is at least one idle thread, the starved count for this
kernel is increased. Otherwise, the kernel’s non-starved count is increased by
one, and the sum of busy threads is increased by the current number of busy
threads.
4.3.3 Updating priorities for apriority
Update algorithm
The update algorithm for apriority is called every so often to modify
the priority adjustments. It happens on a worker thread at the end of
complete-task. More details on the update interval are given below.
The update algorithm works as follows. First, if more than 10% of
tasks were starved; that is, if ∑k sk ≥ 1/10∑k ck, the
main thread is probably the bottleneck, and there is little the adaptive
scheduler can do, except try to minimise overhead. In this case, the priority
adjustments are left unchanged, and the interval to the next time the update
algorithm is called is increased. The experiments in
Section 4.4 simply use an interval of 100ms for the normal
case and 500ms if more than 10% of tasks were starved. This behaviour could be
made more sophisticated.
If fewer than 10% of tasks were starved, a candidate kernel is
identified. The candidate has the lowest average number of busy threads. In
case of ties, it is the kernel with the largest ID, which is the one nearest
the bottom of the stream graph. The average number of busy threads for the
candidate is compared with the average for all kernels. If it is less than
90% of the average for all kernels, then the candidate is treated as a the
bottleneck kernel; otherwise, there is no clear bottleneck kernel.
The priority of the bottleneck kernel is increased by the number of kernels per
iteration. In order to avoid priority inversion, if any of the candidate’s
predecessors now have a lower priority than it, their priorities are increased
to be the same. This procedure applies to all ancestors of the candidate.
After updating any kernel adjustments, all kernels have their statistics reset:
tk := 0, sk := 0, and ck := 0 for all k.
For the example in Figure 4.9, the candidate is kernel
a, its average number of busy threads is 1.0, which is less than 90% of the
average since the average is 3.7. Its priority adjustment is increased to eight,
which correctly pipelines the program. All statistics are reset, no other
priority adjustments are increased, and the program remains correctly pipelined
for the rest of the execution.
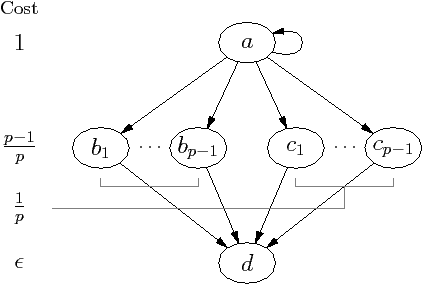
| Figure 4.11: Example showing why all kernel statistics should be reset |
It may seem sufficient, after updating a kernel’s adjustment, to only reset the
statistics for either that kernel or that kernel and its ancestors.
Figure 4.11 is an counterexample to such a claim.
The bottleneck is kernel a, exactly as before. After correctly increasing
the priority adjustment for kernel a, kernel d will next appear to be the
bottleneck. Unfortunately, updating the priority adjustment for kernel d
makes all priority adjustments the same, which has the same effect as if they
were all zero.
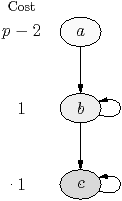
(a) Stream graph
(b) Example trace
| Kernel | Average Busy threads |
| a | p |
| b | 2 | ← |
| c | p |
| d | ≥ p+2/2 |
(c) Statistics for apriority
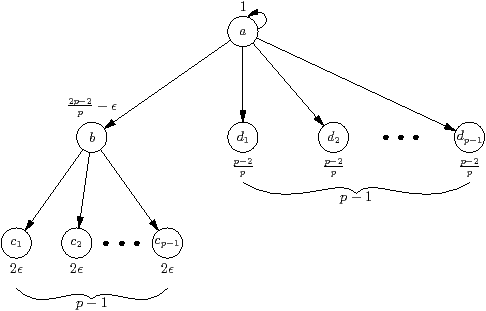
| Figure 4.12: Example that shows the benefit from updating the ancestors, where p is the number of processors |
Updating ancestors
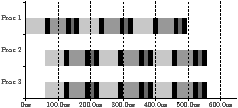
Figure 4.12 is an example that illustrates why the adaptive
algorithms need to update the ancestors of the indicated kernel. Subfigure (a)
is the stream graph. All kernels have multiplicity one, and cost shown outside
the vertex, where p is the number of processors and є ≪ 1 is some
small number much less than one. Since the only stateful kernel is the source,
a, the critical path has cost 1 per iteration.
The total work per iteration is
so an optimal schedule on p processors requires time 1 per iteration.
Subfigure (b) is an example trace of two iterations, using the oldest-first
scheduler. This requires time 2p−1/p+є/2 per
iteration.
Subfigure (c) shows the busy statistics for the apriority scheduler,
which is, for each kernel, the average number of busy processors just as it
finishes, but before any of its predecessors wake up. The startup mechanism
means that even on the first iteration, kernel a registers p busy
processors. The results for b and c are clear. The value for kernel d
is an average: the first kernel d that finishes sees p busy processors, the
second sees p−1 busy processors, and the last sees two busy processors. The
average can be found by pairing off in pairs, starting with the first and last,
and each pair has average p+2/2 busy processors.
The apriority and gpriority schedulers will therefore identify
kernel b as the critical path, and increase its priority. Unfortunately kernel b
already always executes immediately after kernel a in the same iteration, so
increasing its priority makes no difference—it is necessary also to increase the
priority of kernel a.
4.3.4 Updating priorities for gpriority
The gpriority algorithm differs from apriority in the
following ways. First, some decision has to be made about what constitutes a
kernel. Second, the dependency graph between kernels is constructed at
run-time, rather than being provided somehow by the compiler. Third, this
kernel dependency graph may be cyclic. Fourth, there is no concept of a
steady-state iteration.
A reasonable definition of a kernel is the source line of the caller of
the StarSs task. For a stream program, converted using str2oss or a
similar tool, this definition is consistent with apriority. When the
same kernel definition is instantiated several times in a stream graph, each
instantiation is treated as a different kernel.
Figures 5.15
and 5.16 show the translated code for
a stream program: lines 95 and 96 correspond to two different kernels with the
same function definition.
To construct the kernel dependency graph, in create-task, the
scheduler has to map from the task to the kernel. This can be done either by
explicitly adding tags in the compiler, or hashing the address of the work
function. The latter works when the work function is actually a wrapper, which
is the case using the Mercurium source to source compiler for OmpSs.
Figure 4.13 shows an example kernel dependency graph,
constructed by gpriority for 25 frames of HD 1080p video through the
H.264 decoder skeleton. There are four kernels, corresponding to the four
stages in this H.264 decoder skeleton. This benchmark has streaming behaviour,
but it is not one dimensional. Macroblock decode and Deblock
iterate over a two-dimensional space.
To the left of each of kernel is shown the number of times it was called; e.g.
Scan was called 25 times: once per frame. Each edge shows the number
of times, n, that that dependency was seen in the PDG, and the
distance, which is the average difference, D, in task number. For
example, assuming that the tile width is two or more, macroblock decode usually
depends on three of its neighbours: the tile to the left, with difference 1,
the tile above, with difference 31, and the tile above and to the right, with
difference 30.3 The average of these values is 20.7, which is
close to the value that was measured. The measured distance is a little
different, because some of these dependencies are missing at the image borders.
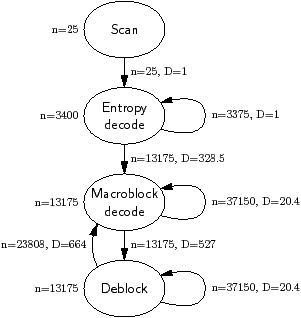
| Figure 4.13: Kernel dependency graph for H.264 decoder skeleton |
The priority of a task is equal to its kernel’s priority adjustment minus the
task number, as for apriority. The priority adjustments for the
kernels control the overlapping of kernels. Each kernel, however, is
effectively scheduled using oldest-first, since all the tasks for the same
kernel have the same adjustment. The gpriority scheduler uses the
same statistics, shown in Figure 4.4, as
apriority. Similarly, the bottleneck kernel is found in exactly the
same manner as before.
Since there is no concept of steady-state iteration, the priority adjustment
for the bottleneck kernel cannot be increased by the number of tasks per
iteration. Instead, each kernel has a delta value, which is initialised
to some small number. Whenever that kernel has its priority adjustment
increased, it is increased by the delta, and the delta is doubled. This
mechanism is rather crude, but it seems to work.
Whenever a kernel is identified as a bottleneck and its priority adjustment is
increased, the adjustments of its ancestors are updated to avoid priority
inversion. For example, if the adjustment of Entropy Decode is
increased from zero to Δ, the adjustment of Scan would be
increased from zero to Δ − 1. Unlike for apriority, this
procedure takes account of the average difference in task number.
After increasing the priority adjustment for kernel k from ak to ak′ =
ak + Δ, each of that kernels predecessors, p, are visited in turn.
The predecessor’s priority adjustment is updated:
|
ap′ = max(ap, ak + Δ − Dpk) where Dpk is the distance of the edge from p to k.
|
The intuition is that priority inversion happens when a task has higher
priority than a predecessor. The difference in priorities of tasks is equal to
the difference in priority adjustment minus the difference in task number.
4.4 Experimental evaluation
Infrastructure and benchmarks
This section describes the experimental results for the schedulers described in
Section 4.2.1, together with the adaptive schedulers
described in Section 4.3. The implementation and results
use OMP Superscalar (OmpSs), but they are not specific to it. The OmpSs
compiler generates an executable that uses the Nanos++ runtime library.
The benchmarks are listed in Table 4.5. The StreamIt
2.1.1 benchmarks [GTA06] are one-dimensional stream programs
written in the StreamIt language. They were converted to StarSs source code
using a conversion tool, known as str2oss, described in
Section 5.3.
At the time of writing, Nanos++ does not yet implement renaming, described in
Section 1.4.1. If each task for a given filter were to write
its output into the same temporary array, there would be output and
anti-dependencies between consecutive iterations. For this reason, a
command-line option was added to str2oss to expand the sizes of the
temporary arrays by a given factor, n, and use the segments in round-robin
order. Each unwanted dependency therefore crosses n iterations rather than
one.
The experimental results include measurements of the peak memory use. This is
the largest amount of memory that would be used for renaming. Since Nanos++
does not actually do renaming, the memory use was modelled by the application.
Benchmark(s) | | Source | | Parameters or input file |
StreamIt 2.1.1 benchmarks | | MIT | | Twelve benchmarks in StreamIt language |
Check LU factorisation | | SMPSs 2.1 | | Block size: 32× 32, matrix size: 16× 16 blocks |
Cholesky factorisation | | BSC | | Block size: 32× 32, matrix size: 16× 16 blocks |
H.264 decoder skeleton, supporting 3D wave | | Self | | 100 frames of Pedestrian (1080p) from HDVideoBench [ASRV07] |
| Table 4.5: Benchmarks used in the evaluation |
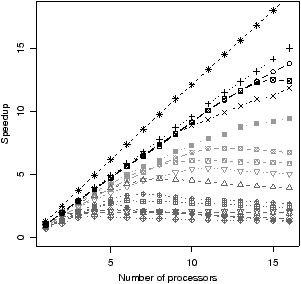 | 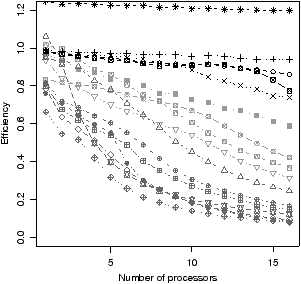 |
| (a) Speedup | (b) Efficiency = speedup / num. processors |
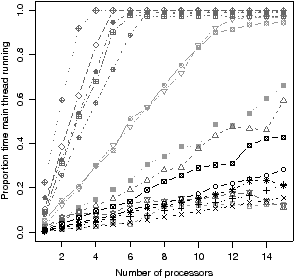 |
| (c) Fraction of time main thread is running |
| Figure 4.14: Scalability of the benchmarks |
There are four additional benchmarks written in StarSs. Check LU factorises a
non-symmetrical matrix into the product of a lower-triangular and an
upper-triangular matrix, without a permutation matrix: A=LU. It was taken
as-is from the SMP Superscalar 2.1 distribution, including a correctness check
at the end, which is the sparse matrix multiplication of L and U. Cholesky
uses LAPACK and BLAS routines to perform a Cholesky decomposition: A=LLT.
The H.264 decoder skeleton has the same pattern of dependencies as an H.264
decoder using the 3D wave optimisation [MAJ+09]. The
entropy decoder was unrolled by 60 macroblocks, and the macroblock decode and
deblocking tasks were unrolled by four in each direction, using the standard
tile shape.
Scalability
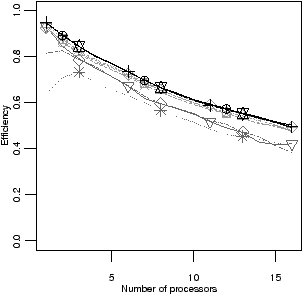
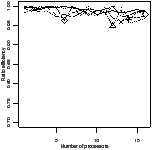
Figure 4.14 shows how well the benchmarks scale, as the number of
processors varies between one and sixteen. The comparison is between the best
dynamic scheduler and a serial implementation, compiled with GCC instead of the
OmpSs compiler. The best scheduler is chosen independently for each data
point, in order to estimate the scalability of the application itself.
It is clear that across the benchmarks there is a wide range of scalability:
filterbank scales exceptionally well. Five benchmarks have 80% or
higher efficiency to sixteen cores. Other benchmarks, especially des,
have poor scalability. As can be seen from Figure 4.14(c), most
of the benchmarks that scale poorly have the main thread running for a large
proportion of time. This shows that for these benchmarks the main thread is
the bottleneck.
The reason why some benchmarks have especially poor performance is that,
although the benchmarks have been optimised using kernel unrolling, they have
not benefited from kernel fusion. This is because the str2oss tool
described in Section 5.3 supports unrolling but not fusion. This is
evidence that a partitioning algorithm like that in Section 3.2
is still beneficial, even with dynamic scheduling.
Nevertheless, the wide range of scalability means that the results of this
section are applicable both to benchmarks that scale well and benchmarks that
scale poorly.
Average and worst-case results
Average
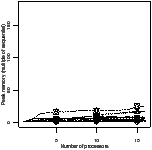
Figure 4.15(a) and (b) show, for each
scheduler, the average utilisation and average peak memory use, where the
average is taken across all streaming benchmarks. The non-streaming
benchmarks were excluded, since they are not supported by wave and
apriority. The memory use is the multiple of that required by the
sequential version of the benchmark. It includes all data regions used by the
benchmark and renamed by the run-time, but it excludes data structures used by
the run-time itself; for example to store the PDG.
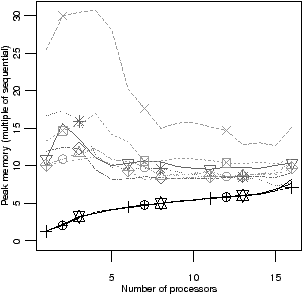
Three heuristics have consistently poor average performance, between 7% and
10% worse than oldest and the two adaptive policies. These are
botlev, crit, and mdesc; all of which suffer due to
the overhead of recalculating the bottom level or the number of descendants as
the PDG is built.
The averaged peak memory footprint shows a wide range: toplev is
particularly prone to poor back pressure, causing excessive average memory use.
The oldest, apriority and gpriority schedulers have
considerably lower memory use than the others, since these schedulers tend to
overlap few stream program iterations.
| Average across benchmarks |
| |
(a) Mean efficiency |
(b) Geometric mean peak memory
|
| Worst benchmark |
| |
(c) Relative efficiency | |
| Figure 4.15: Average and worst case results |
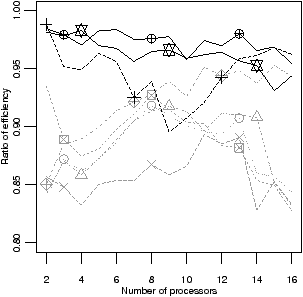
| Figure 4.16: Worst case results: detail of efficiency of most robust schedulers |
Robustness
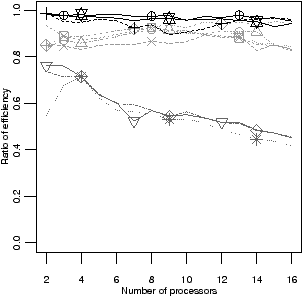
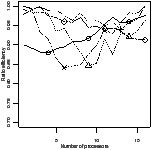
Figure 4.15(c) and (d) compares the
robustness of the schedulers. In Figure 4.15(c), each data
point is the worst case ratio of efficiency, which is the efficiency of the
scheduler, divided by the efficiency of the best scheduler, for that benchmark
and number of processors. The worst case is found across the streaming
benchmarks. A value of 1.0 on the y-axis therefore indicates that, for all
benchmarks, the scheduler achieves the best performance seen.
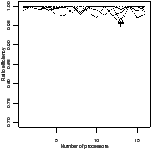
Figure 4.16 shows the same results, but magnified to show only the
efficiency of the more robust schedulers.
Figure 4.15(d) is the worst case memory use, as a multiple
of the sequential version. As before, the worst case is found across all
streaming benchmarks.
As before, botlev, crit and mdesc are clearly the
worst-performing schedulers, again due to the overhead of calculating the
bottom level or number of descendants.
The only robust schedulers are the adaptive schedulers, apriority and
gpriority. Of the non-adaptive schedulers, oldest is best
performing overall, but its worst efficiency is up to 8% lower.
The worst case peak memory footprint shows a wider range: toplev,
fifo, and lifo have excessive memory use for certain
benchmarks. The remaining heuristics have intermediate memory use, which is
considerably higher than that of oldest, apriority, and
gpriority. Compared with oldest, the two adaptive schedulers
use a negligible amount of additional memory.

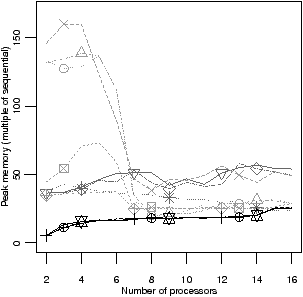
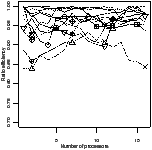
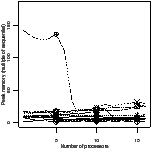
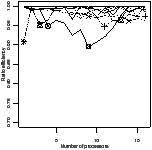
Ratio efficiency | Peak memory | Ratio efficiency | Peak memory |
| | | | |
| | | |
| (a) fifo | (b) oldest |
| |
| | | |
| (c) toplev | (d) wave |
| |
| | | |
| (e) apriority | (f) gpriority |
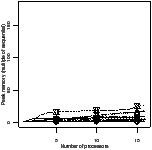
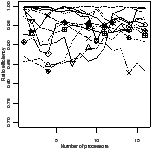
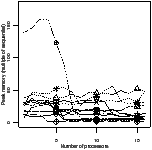
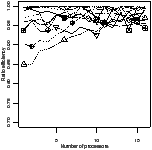
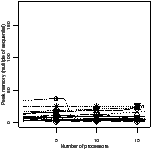
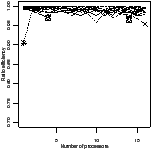
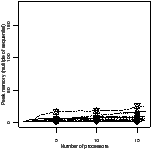
| Figure 4.17: Comparison of the scheduling heuristics: StreamIt |

| | | |
(a) fifo | (b) oldest | (c) toplev | (d) gpriority |
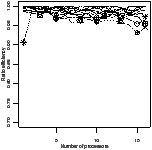
| Figure 4.18: Comparison of the scheduling heuristics: non-StreamIt |
Detailed results
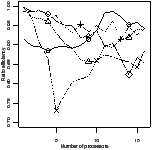
This section compares the efficiency and memory use of the six best schedulers.
These are fifo, oldest, toplev, wave, and
the two adaptive schedulers: apriority and gpriority. The
other schedulers were seen to have poor robustness and average performance.
Figure 4.17 shows the experimental results for the
StreamIt benchmarks. There are two plots for each scheduler. The first is the
ratio of efficiency: the efficiency of that scheduler divided by the efficiency
of the best scheduler for the same benchmark and number of processors. The y
axis has been expanded to show greater detail—no points were lost in doing
so. The second plot is the peak memory use, as a multiple of the sequential
version.
The apriority scheduler has the highest efficiency and lowest memory
use. The gpriority scheduler has slightly lower efficiency due to the
greater overhead, and the same low memory use.
Figure 4.18 shows the experimental results for the
non-StreamIt benchmarks. The wave and apriority schedulers
were excluded, since they both require regular stream programs, so do not
support these benchmarks. It was not possible to determine the memory
footprint, because Nanos++ does not currently implement renaming. As described
in Section 4.4, the renaming memory footprint was
modelled by the application, and this was only implemented for the StreamIt
benchmarks.
The gpriority scheduler has the best efficiency and memory use overall.
4.5 Conclusions
This chapter introduced two new low-complexity adaptive dynamic scheduling
algorithms for stream-like programs. Many existing scheduling algorithms,
listed in Table 4.1, either schedule the whole program in
advance, or they need to know the execution time of every task in advance, or
they are too slow.
The scheduling algorithms in this chapter have better average and worst-case
performance than all the scheduling algorithms in Table 4.2. The
scheduling overhead at run-time is similar to that of oldest-first. They take
advantage of the stream graph representation, by giving each kernel in the
stream graph its own priority adjustment.